농 위키

Part 1. Key Concepts and Terminology

마지막 수정 시각: 2023-07-24 09:25:45

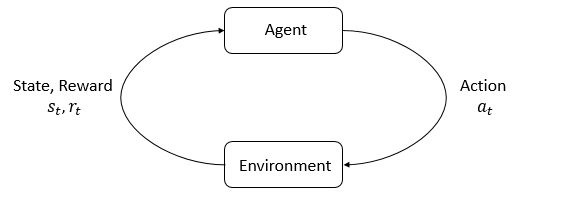
agent, environment 두 가지가 핵심적인 개념. environment가 agent가 활동하고 상호작용하는 곳. agent는 매 단계마다 environment의 상태를 확인하고, 어떤 액션을 취할지 선택한다. 이 행동에 따라 환경의 상태가 바뀐다(혹은 알아서 혼자 바뀔 수도 있음).

에이전트는 현재 상태가 얼마나 좋은지, 나쁜지에 대한 정보를 가리키는 수로 표현된 reward 신호도 전달받는다. agent의 목표는 누적된 reward값을 최대화하는 것(=return이라고 불림)이며, 강화학습은 이를 달성하기 위한 행동을 agent한테 가르치는 방법임.

RL이 하는 일에 대해 다루려면 아래 용어들에 대해 더 얘기할 필요가 있다.

States and Observations

state \(s\)는 환경의 모든 정보를 포함하는 것(숨겨진 부분이 없어야 함). 반면, observation \(o\) 는 상태의 부분 집합이다(일부 정보가 숨겨져 있을 수 있음. 스타크래프트의 전장의 안개같은걸 생각해보자).

deep RL에서, state와 obseravtion은 실수 벡터, 행렬, higher-order tensor로 표현된다. 예를들어 시각적인 관찰 정보는 그 픽셀 값들의 RGB 행렬로 표현될 수 있다. 로봇의 상태는 관절의 각도와 속력으로 표현될 수 있고.

agent가 환경의 완전한 상태를 관찰할 수 있다면 환경이 fully observed라고 이야기하고, 일부만 볼 수 있다면 환경이 partially observed라고 이야기한다.

Action Spaces

주어진 환경에서 할 수 있는 모든 가능한 행동들의 집합을 action space라고 부른다. 환경에 따라 유한한 개수의 action만이 허용될 수 있는데(바둑 등), 이런 경우 discrete action sapces라고 부르고, 실 세계에서의 로봇 조작과 같이 무한한 행동 집합을 가지는 경우 continuous action spaces라고 부른다. continuous action sapce에서는 action은 실수 벡터가 된다.

이런 차이에 따라 사용할 수 있는 알고리즘이 달라질 수 있다.

Policies

policy 는 agent가 어떤 액션을 취할지 선택할 때 사용되는 규칙이다. 이는 deterministic할 수 있고, 이 때 일반적으로 \( \mu \) 로 표시한다.

\[ a_t = \mu(s_t) \]

혹은 확률적일수도 있는데, 이 때는 \( \pi \) 로 표시한다.

\[ a_t \sim \pi(\cdot | s_t) \]

policy가 agent의 두뇌와 같은 역할이라 그냥 policy를 agent를 대신하는 표현처럼 쓰기도 한다.

deep RL에서는, parameterized policies를 다룬다. 이는 policies의 출력이 어떤 parameter의 set(예를 들자면 뉴럴 네트워크의 weights, bias 등) 에 의존하는 계산 가능한 함수인 것을 의미한다. 이럴때 policy의 parameter를 강조하기 위해 아래와 같은 subscript로 표현할 수 있다.

\[ a_t = \mu_{\theta}(s_t) \]

\[ a_t \sim \pi_{\theta}(\cdot | s_t) \]

Trajectories

trajectory는 월드의 상태와 액션의 시퀀스를 말한다.

\[ \tau = (s_0, a_0, s_1, a_1, ...) \]

첫 상태가 \(s_0\)이고, 이는 start-state distribution에서 무작위로 샘플링된 상태이다. 가끔 start-state distribution은 \(p_0\)으로도 표기된다.

\[ s_0 \sim \rho_0(\cdot) \]

어떤 시간 \(t\)에서의 상태 \(S_t\)와 \(t+1\)에서의 상태 \(S_{t+1}\)에 대해, 환경의 특성에 따라 \(S_{t+1}\)은 \(S_t\)와 \(a_t\)(가장 최근의 action)에 의해서 결정된다. 이게 deterministic한 경우,

\[ s_{t+1} = f(s_t, a_t) \]

로 표현하고, stochastic한 경우

\[ s_{t+1} \sim P(\cdot|s_t, a_t) \]

로 표현한다. action은 agent가 따르는 policy로부터 나온다. trajectories는 episodes 혹은 rollouts로도 불림.

Reward and Return

reward function \(R\)은 강화학습에서 매우 중요하다. 이는 환경의 현재 상태, 취해진 액션, 그리고 다음 상태에 의존한다.

\[ r_t = R(s_t, a_t, s_{t+1}) \]

그냥 현재 상태에만 의존하거나 현재상태-행동의 페어에만 의존하는 등으로 단순화될 때도 있다. \(r_t = R(s_t)\) 거나 \(r_t = R(s_t, a_t)\)인 경우.

agent의 목적은 trajectory에 따른 누적 reward의 개념을 최대화하는 것.

return의 종류중 하나로 finite-horizon undiscounted return이 있다. 이는 고정된 steps의 window로부터 합해진 reward를 뜻한다.

\[ R(\tau) = \sum_{t=0}^T r_t \]

다른 종류로는 infinite-horizon discounted return이 있다. 이는 agent로부터 얻어진 모든 reward의 합이되, 미래로 갈수록 합이 discount되는 것. 이 공식은 (0, 1)범위의 실수인 discount factor를 포함한다.

\[ R(\tau) = \sum_{t=0}^{\infty} \gamma^t r_t \]

직관적으로, 지금 현금을 가지는게 나중에 현금을 가지는 것보다 낫다. 수학적으로, infinite-horizon sum은 수렴하지 않을 수 있고, 이는 다루기가 어렵다. discount factor와 reasonable한 조건 하에서는 infinite sum이 수렴하므로 다루기가 쉬울것.

The RL Problem

RL의 목표는 return의 기댓값을 최대화하는 policy를 찾는 것. return의 기댓값을 얘기하려면, 먼저 trajectories의 확률 분포에 대해 얘기해야한다.

환경의 transition과 policy가 전부 확률적이라고 하자. 이 경우, T-step trajectory의 확률은 다음과 같다.

\[ P(\tau|\pi) = \rho_0 (s_0) \prod_{t=0}^{T-1} P(s_{t+1} | s_t, a_t) \pi(a_t | s_t) \]

초기 상태의 확률 분포로부터 초기 상태를 뽑고, 다시 여기에서 각 상태-행동과 그 상태-행동이 나올 수 있는 확률들을 전부 곱하면 타임 \(T\)까지 이어지는 trajectory의 확률이 나올 것이다.

이 상태에서, return의 기댓값은 다음과 같은 식으로 나타낼 수 있다.

\[ J(\pi) = \int_{\tau} P(\tau|\pi) R(\tau) = E_{\tau\sim \pi}{R(\tau)} \]

모든 상태 분포에 대해 확률과 그때의 리턴값을 곱한것을 합한 것. RL의 중심 최적화 문제는 따라서

\[ \pi^* = \arg \max_{\pi} J(\pi) \]

로 표현할 수 있다. 즉, \(J(\pi)\) 를 최대화하는 \(\pi\) (agent의 행동 확률 분포)를 찾는 것. 이 때의 \( \pi^* \)를 optimal policy라고 부른다.

Value Functions

상태, 혹은 상태-행동 페어의 가치(value)를 아는 것이 유용할 때가 종종 있다. value는 특정 상태, 혹은 상태-행동 페어로부터 시작해서 특정 policy에 따라 쭉 진행했을 때 얻게될 return의 기댓값을 뜻한다. value functions는 거의 모든 RL 알고리즘에 쓰인다.

여기에는 중요한 4가지 함수가 있다.

1. On-Policy Value Function. 이는 상태 \(s\)에서 시작해서 영원히 policy \(\pi\)를 따라 행동했을 때 얻게될 return의 기댓값을 준다.

\[ V^{\pi}(s) = E_{\tau \sim \pi}\{R(\tau)| s_0 = s\} \]

2. On-Policy Action-Value Function. 이는 상태 \(s\)에서 특정 행동 \(a\)(policy를 따르지 않는 행동일 수 있음)를 취한 후 계속해서 policy를 따라 행동했을 때 얻게될 return의 기댓값을 준다.

\[ Q^{\pi}(s,a) = E_{\tau \sim \pi}\{R(\tau)| s_0 = s, a_0 = a\} \]

3. Optimal Value Function. 상태 \(s\)에서 시작해서 optimal policy를 따라 계속 행동했을 때 얻게 될 기댓값을 준다.

\[ V^*(s) = \max_{\pi} E_{\tau \sim \pi}\{R(\tau)| s_0 = s\} \]

4. Optimal Action-Value Function. 상태 \(s\)에서 시작해서, 특정한 행동 \(a\)를 취한 후, optimal policy를 따랐을 때 얻게될 기댓값을 준다.

\[ Q^*(s,a) = \max_{\pi} E_{\tau \sim \pi}\{R(\tau)| s_0 = s, a_0 = a\} \]

The Optimal Q-Function and the Optimal Action

optimal action-value function과 optimal policy에 의해 선택되는 action 사이에는 아주 중요한 연관이 있다. 정의에 의해, optimal action-value function은 \(s\)에서 시작해서 임의의 행동 \(a\)를 선택한 후, optimal policy를 따랐을 때의 기댓값을 준다.

\(s\)에서의 optimal policy는 \(s\)에서 시작했을 때 가능한 기댓값의 최대를 고른다. 따라서, optimal aciton-value function을 안다면 이로부터 optimal action도 바로 구할 수 있다.

\[ a^*(s) = \arg \max_a Q^* (s,a) \]

Bellman Equations

이 4종류의 value function들은 Bellman equations이라 불리는 특수한 self-consistency equation을 만족한다. bellman equations의 기본적인 아이디어는 다음과 같다.

\[ V^{\pi}(s) = E_{a \sim \pi \\ s'\sim P}\{r(s,a) + \gamma V^{\pi}(s')\} \\ Q^{\pi}(s,a) = E_{s'\sim P}\{r(s,a) + \gamma E_{a'\sim \pi}{Q^{\pi}(s',a')}\} \]

\(V\)와 \(Q\)는 \(a\)가 고정이냐 아니냐의 차이가 있어서 \(max\)의 위치가 바뀐다는 점에 유의. \(V\)의 경우 \(a\) 행동을 무엇을 할지 최적화지만, \(Q\)의 경우 \(a\)까지는 고정하고 그 이후 상태에서의 최댓값이 기준이 되므로 \(max\) 함수가 들어가는 위치가 바뀐다.

Advantage Functions

RL에서, 어떤 행동이 정확히 기술할 필요는 없고, 평균적으로 다른것보다 얼마나 좋은지만 기술해도 된다. 즉, 그 행동의 상대적인 advantage를 알고 싶은 것.

advantage function은 수학적으로 다음과 같이 정의된다.

\[ A^{\pi}(s,a) = Q^{\pi}(s,a) - V^{\pi}(s) \]

\(V(s)\)가 상태 \(s\)에서 얻을 수 있는 기댓값이고, \(Q(s,a)\)가 \(s\) 상태에서 \(a\)를 골랐을 때 얻을 수 있는 기댓값이므로, 이 차이가 advantage가 되는 것은 직관적.

Formalism

agent의 environment를 좀 더 formal하게 정의해보자. markov decision process(MDP)는 5-tuple \((S,A,R,P,p_0)\)으로 표기된다.

markov decision process는 이 시스템이 markov property를 만족한다는 점에서 유래한 이름이다. 즉, transition은 항상 가장 최근의 행동과 상태에만 의존하며, 이전의 히스토리에 영향을 받지 않는다.