농 위키

그래프 개형을 이용한 DP 최적화(slope trick)

마지막 수정 시각: 2020-10-29 21:12:08

\(N\)개의 숫자로 이루어진 배열이 주어진다(\(N \le 3000\)). 각 숫자는 \(1\)이상 \(3000\) 이하의 정수다.

이 때, 한 번의 연산을 통해 배열에서 임의 위치의 숫자 값을 \(1\) 증가시키거나 \(1\) 감소시킬 수 있다. 연산을 적용한 후에도 배열의 각 위치의 값은 \(1\) 이상 \(3000\)이하여야 한다.

주어진 배열을 오름차순으로 만들기 위해 최소 몇 번의 연산이 필요할까?

예를 들어, 2 3 9 7 9 가 주어질 경우 3번의 연산을 통해 2 3 7 8 9 로 바꿔 오름차순을 만들 수 있고 이 경우가 최소다.

위 문제는 아주 간단한 DP로 풀 수 있다.

라고 정의하자. 이렇게 할 경우, \[ DP(x, k) = \min(DP(x-1, k-1), DP(x-1, k-2), \cdots, DP(x-1, 1)) + |A_x - k| \]로 식을 유도할 수 있다.

왜냐하면 일단 내 위치의 값을 \(k\)로 만들기 위해 \(|A_x - k|\)번의 연산이 필요하고, 이 때 배열에서 내 바로 앞 위치까지의 값은 전부 오름차순이면서 \(k\)보다는 작은 값이어야 하기 때문이다. 즉, \(DP(x-1,k-1), DP(x-1, k-2), \cdots, DP(x-1, 1)\)중에서 연산 횟수가 최소로 드는 것을 고른 후 거기에 \(|A_x - k|\) 를 더한 것과 같아진다.

물론 답이 될 수 없는 경우 등 적당한 예외 처리를 추가해 주어야겠지만 아무튼 대충 이와 같은 방법을 통해 \(O(NX)\) (\(X\)는 배열 원소에서 가능한 최대 값 크기) 시간에 해결하는게 가능하다.

이렇게 해결하는 방법은 생각하기도 풀기도 별로 어렵지 않다. 그러면 여기서 조건을 약간 바꿔보자. 연산을 적용한 후에도 배열의 각 위치의 값은 \(1\)이상 \(3000\)이하여야 한다 라는 조건이 빠지면 어떨까? 이 경우에도 사실 각 위치에서 가능한 높이 값은 \(-3000\) ~ \(6000\) 정도이기 때문에 이 경우들을 다 확인해보면 된다. 따라서 이 조건이 빠져도 \(O(NX)\) 시간에 마찬가지로 해결 가능하다(물론 코드가 좀 더 지저분해질 것이다).

그럼 좀 더 화끈하게, 각 숫자가 \(-10^9\) 에서 \(10^9\) 범위까지 가능하다고 하자. 더 나아가서, \(N \le 3000\)이 아니라 \(N \le 10^6\)이라고 하자. 이렇게 되면 문제를 해결하기가 굉장히 막막해진다.

하지만 이렇게 입력의 크기가 굉장히 커지는 경우에도, 주어진 DP 점화식이 가지는 그래프 개형을 이용한 독특한 최적화를 통해 문제를 \(O(NlogN)\)에 해결할 수 있다. 나름대로 널리 알려진 테크닉인 것 같은데 이 테크닉을 가리키는 별도의 이름이 있는지는 모르겠어서 제목도 그냥 그래프 개형을 이용한 DP 최적화라고 썼다(+수정 - 코드포스에 slope trick이라는 이름의 튜토리얼 글이 있다.)

자, 아무튼 이제 이 문제를 어떻게 하면 \(O(NlogN)\)으로 최적화할 수 있는지 알아보자. 바로 윗 문단에서 말한 것처럼, 이 최적화는 DP 식을 그래프 형태로 나타냈을 때의 개형을 바탕으로 하는 최적화다. 그러니 한 번 그래프 개형을 살펴보자. \(DP(x, k)\)는 인자 2개를 요구하니 그냥 그리면 그래프는 3차원이 될 것이다. 이걸 그리는 건 너무 힘들고 생각하기도 힘들다.. 그러니, \(x\) 값을 고정하고 순차적으로 \(DP(1,k)\) 부터 \(DP(2,k), DP(3,k), \dots, DP(n, k)\)가 각각 어떤 형태의 그래프를 가지는지 먼저 확인해보자.

우선 제일 간단한 \(DP(1,k)\)의 개형을 살펴 볼 차례다. \(DP(1,k) = |A_1 - k|\) 이므로 \(k\) 값에 따른 \(DP(1,k)\) 값의 변화는 아주 간단하다. 그림으로 나타내면 다음과 같다.

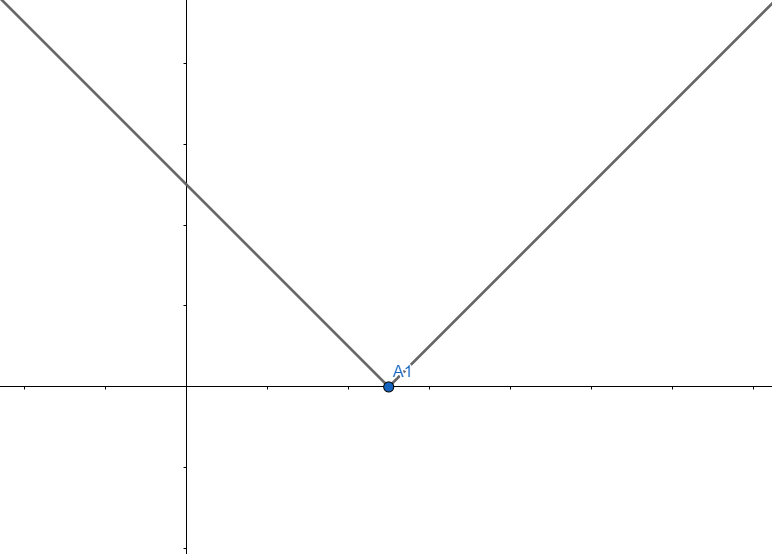
흔히 볼 수 있는 절댓값 그래프 형태이다. \(k = A_1\)일 때 그래프의 값이 최소가 된다는 것도 확인할 수 있다. 다음은 \(DP(2,k)\) 그래프의 개형을 살펴볼 차례다. \(DP(2,k)\)는 식으로 나타내면 \(\min_{j \lt k} {DP(1,j)} + |A_2 - k|\) 가 되는데, 이 식을 한 번에 표현하려고 하면 좀 복잡하니 덧셈을 기준으로 앞 뒤를 나눠서 생각해보자.

여기서 \(\min_{j \lt k}{DP(1,j)} \) 그래프는 독특한 특징이 있다. 이 식은 결국 어떤 \(k\)에 대해 \(k\)의 왼쪽에서 가장 작은 \(DP(1,j)\)를 선택하겠다는 뜻인데, \(DP(1,j)\)가 절댓값 그래프이기 때문에 \(k \le A_1\)인 경우 \(DP(1, k-1)\)과 값이 같고 \(k \gt A_1\)인 경우 \(DP(1, A_1)\)과 같은 값을 가지는 식이 된다. 즉, 최솟값이 되는 위치 오른쪽으로는 일직선으로 바뀐다. 그림으로 나타내면 다음과 같다.

원래 그래프가 검은색, \(k\) 값에 따른 \(\min_{j \lt k}{DP(1,j)} \) 값 그래프가 빨간색 그래프이다. 이제 여기에 \(|A_2 - k|\) 그래프를 더해보자. 이 때, \(A_2 \le A_1\) 인 경우와 \(A_2 \gt A_1\)인 경우가 서로 조금 다른 형태를 가질 것이다. 하지만 지금 우리는 대략적인 그래프 개형을 살펴보는 과정을 통해 최적화에 필요한 직관을 얻고자 하는 것이므로 \(A_2 \le A_1\)라고 가정하고 생각하자. 나머지 경우는 나중에 풀이를 구체화하면서 자세히 다루게 될 것이다.

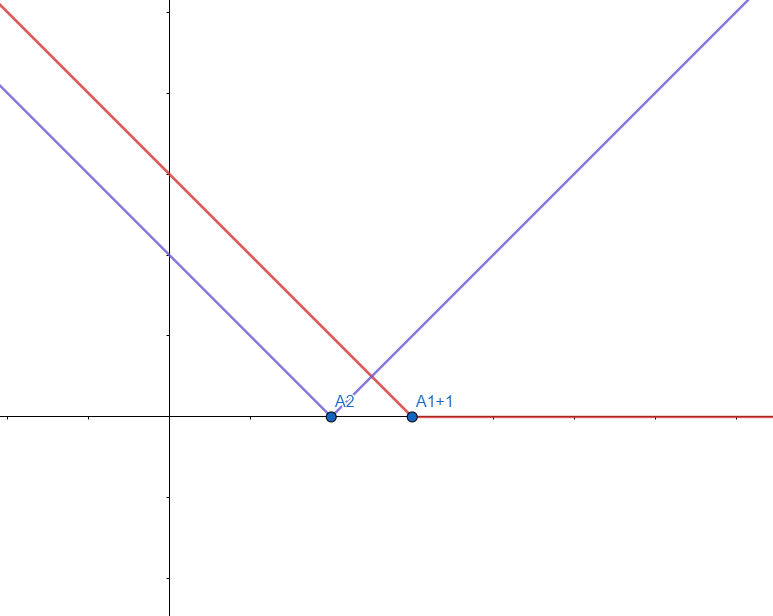
이 경우는 이런 두 그래프의 합이 될 것이다. 앞의 보라색 그래프가 \(|A_2 - k|\) 그래프다. 이 그래프들의 값을 서로 더하면, 구간이 세 가지로 나뉜다. 우선 \(k \le A_2\) 인 경우는 기울기가 \(-2\) 인 그래프가 될 것이고, \(A_2 \lt k \le A_1 + 1\) 인 구간의 경우 기울기가 \(0\)인 그래프가 될 것이고, \(A_1 + 1 \lt k\) 인 구간의 경우 기울기가 \(1\)인 그래프가 될 것이다. 두 그래프를 더한 그래프를 그림으로 그리면 다음과 같다.

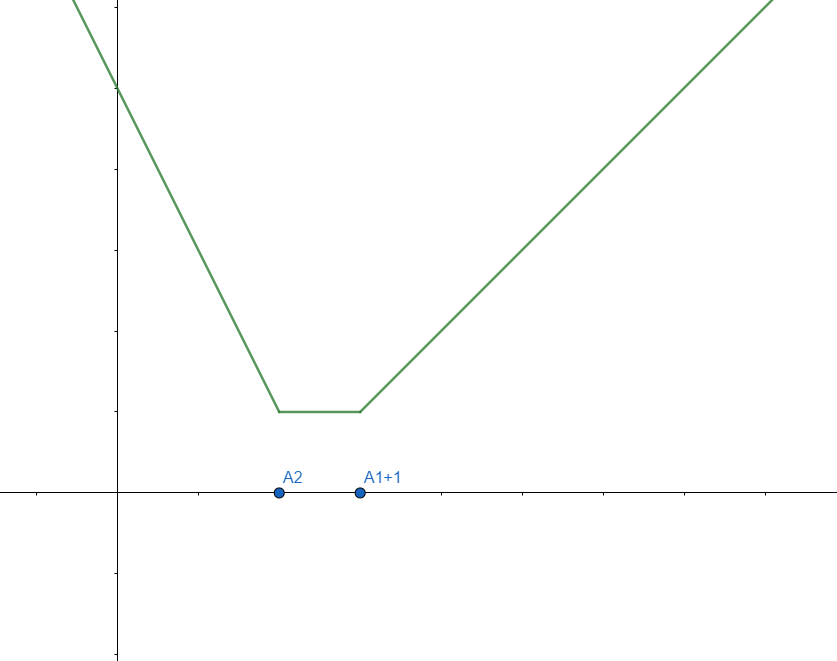
뭔가 \(DP(1, k)\) 랑 그래프가 비슷한 것 같긴 한데 아직은 감이 잘 안 온다. 그러니 \(DP(3, k)\)까지 한 번 확인해보자.

\(DP(3, k)\) 는 동일한 점화식을 통해 \(\min_{j \lt k}{DP(2,j)} + |A_3 - k|\)로 표현할 수 있다. 이것도 역시 두 가지 함수의 합이므로 따로 따로 나눠서 생각한 뒤 더해보자.

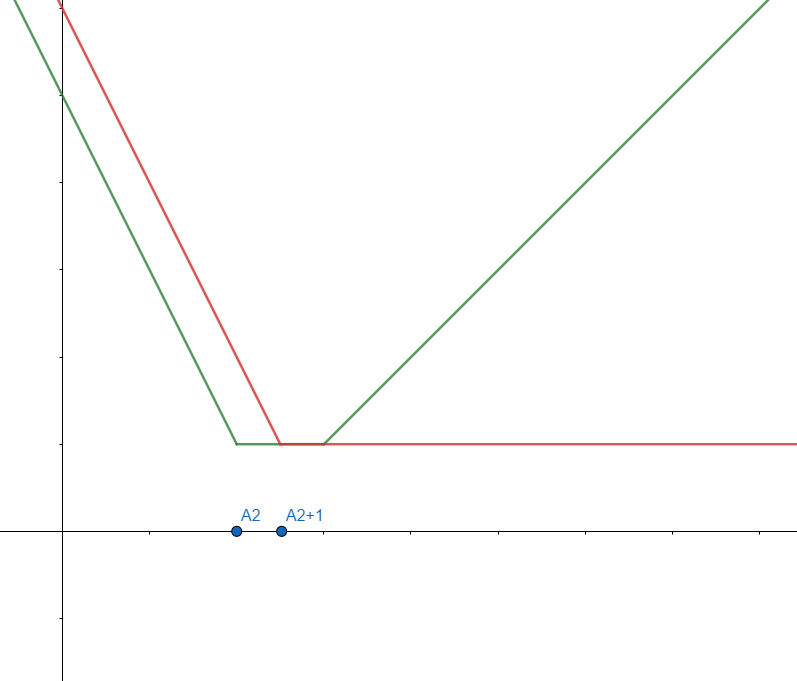
똑같은 원리에 의해, \( min_{j \lt k}{DP(2,j)} \) 그래프는 \(DP(2,k)\) 그래프를 한 칸 우측으로 이동시킨 뒤, 최솟값에 도달한 뒤로는 일직선이 되는 그래프 형태로 바뀐다는 것을 알 수 있다.

여기에 \( |A_3 - k| \) 를 더하는 경우를 생각해보자. 이번엔 아까랑 반대로 \( A_3 \gt A_2 \) 라고 가정한다.

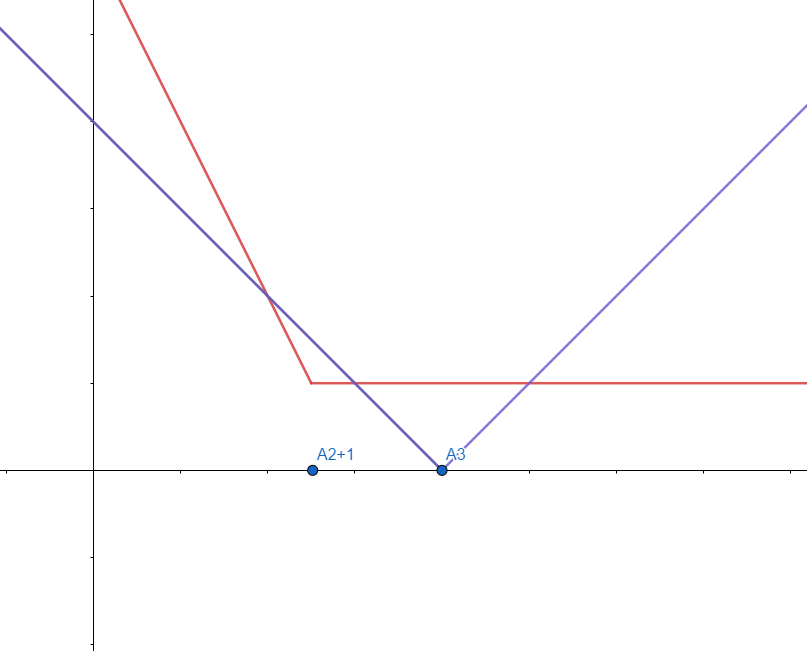
역시 아까랑 비슷하게 구간이 나뉜다. \( k \le A_2 + 1 \) 인 경우, \( A_2 + 1 \lt k \le A_3 \) 인 경우, \( A_3 \lt k \) 인 경우 각각 구간마다 기울기가 다른 세 가지의 직선 그래프가 나타날 것이다.

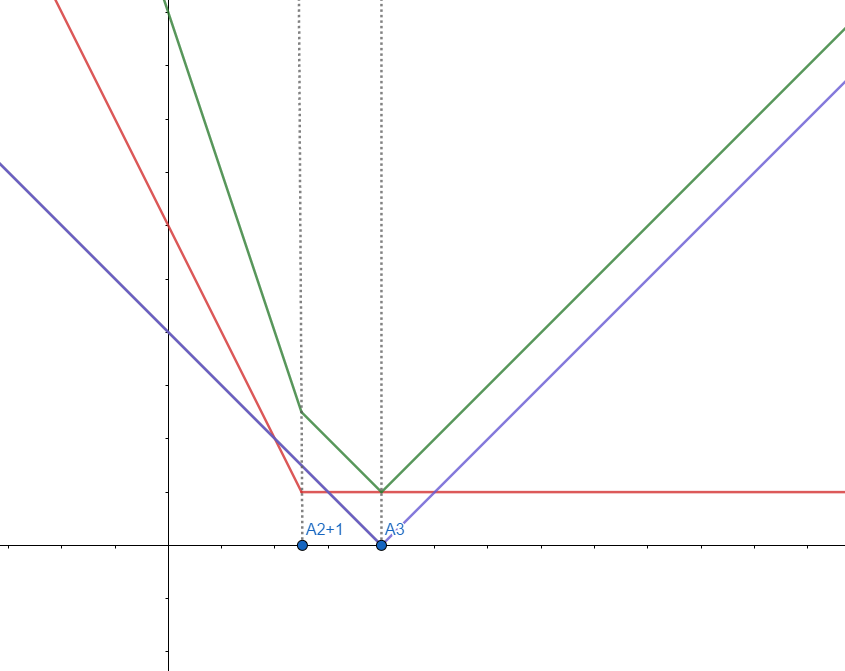
초록색 부분이 실제로 두 그래프를 더한 개형, 그러니까 \(DP(3, k)\)의 개형이다. 이제 뭔가 성질이 조금 보이는 것 같다.

우선, \(DP(n,k) = \min_{j \lt k}{DP(n-1,j)} + |A_n - k| \) 에서 \(\min_{j \lt k}{DP(n-1,j)} \) 부분은 항상 \(DP(n-1,k)\) 그래프에서 최솟값이 되는 지점 오른쪽을 전부 날리고(일자 그래프로 만들고), 그래프 전체를 한 칸 오른쪽으로 미는 것과 동일하다.

또 여기서 \( |A_n - k| \) 를 더하는 동작은, \( A_n \) 을 기준으로 \( A_n \) 좌측의 모든 그래프의 기울기를 \(1\) 감소, \( A_n \) 우측의 모든 그래프의 기울기를 \(1\) 증가시켜주는 역할을 한다. 여기서 한 가지 중요한 사실은 최솟값이 되는 지점 우측의 기울기가 \(0\) 보다 큰 부분은 신경 쓸 필요가 없다는 것이다. 어차피 이쪽 지점은 최솟값이 될 수가 없기 때문이다( \(\min_{j \lt k}{DP(n-1,j)}\) 를 계산할 때 최솟값이 되는 지점 우측은 전부 일직선이 되는 걸 생각해보자. 이쪽 부분은 최솟값보다 답이 더 증가하기만 하므로 신경쓸 필요가 없다). 그러니 최솟값 우측 부분 그래프는 무시하고 일직선으로 둔다.

이제 \(DP(n-1,k)\) 의 그래프를 구해놓은 상태에서 \(DP(n, k)\)의 그래프를 계산하는 상황을 고려해보자. 그래프를 구해놨다는 것은 \(DP(n-1,k)\)에서 각 \(k\) 구간별 직선 기울기와 함숫값을 모두 알고 있다는 뜻이다.

이렇게 생각하면 \(DP(n, k)\)의 그래프 형태는 1. \(DP(n-1,k)\) 그래프를 전부 한 칸 오른쪽으로 평행 이동하고, 2. \(A_n\) 왼쪽 위치의 직선들에 대해 기울기를 전부 \(1\) 감소 시킨 형태가 된다는 것을 알 수 있다.

이렇게 구간별 직선을 관리하면 모든 직선들 중 가장 오른쪽 끝 위치에서의 함숫값이 곧 최솟값(정답)이 된다(이 위치보다 오른쪽 위치에 대해 함숫값은 항상 증가하므로). 따라서, 이 구간별 그래프 형태 및 함숫값을 빠르게 잘 관리할 수 있는 방법만 찾으면 문제를 빠르게 해결할 수 있다.

여기서 등장하는 것이 바로 힙(우선순위 큐)을 응용하는 것이다. 힙에 들어가 있는 각각의 숫자 \(k\)는 그래프에서 \(k\) 왼쪽 직선의 기울기를 1 감소시킨다 라는 의미를 가진다고 하자. 이러면 우선순위 큐에서 제일 위에 있는 값(가장 큰 값) 위치에서의 함숫값이 곧 정답이 되며, \(A_n\) 왼쪽 지점의 기울기를 전부 \(1\) 감소시키는 것은 단순히 큐에 \(A_n\)을 집어넣는 것과 동치가 된다.

문제 해결 과정을 좀 더 구체적으로 정리해보자. 이 문제를 해결하기 위해선 세 종류의 값을 관리해야 한다.

맨 처음에 \(Q\)에는 \(A_1\) 이 들어가고, \(ans\)와 \(t\)는 모두 \(0\)이다. 이제 \(A_1, \dots, A_n\)의 각각의 \(A_i\) 대해서 순서대로 다음 동작을 반복한다.

아까 언급했던 것처럼 두 가지 경우에 따라 식 변화가 조금 다르다. 두 가지 경우를 모두 살펴 보자.

\( r \le A_i\) 인 경우

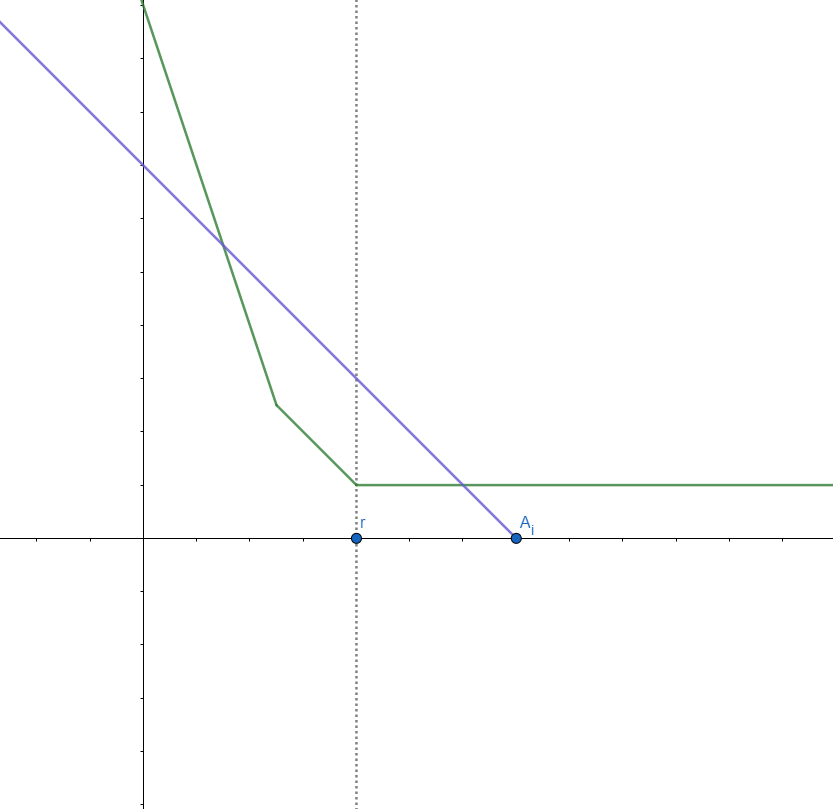
그림으로 보면 이렇다(\(A_i\) 우측 변화량은 안 봐도 되니 무시). 이 경우는 사실 굉장히 간단한데, 그림에서 바로 알 수 있듯이 함숫값의 맨 오른쪽 끝 부분(최솟값 지점)이 \(A_i\) 지점으로 바뀌고, \(A_i\) 왼쪽의 모든 직선들에 대해 기울기가 \(1\) 감소하게 된다.

즉, 이 경우는 \(Q\)에 \(A_i-t\) (\(t\) 좌우 이동량 만큼 더해서 꺼내게 되므로 빼서 넣어줘야 값이 맞다) 를 추가하기만 하면 된다. 따라서 큐에 push 작업 한번만 해주면 되므로 \(O(logN)\) 시간이면 충분하다.

\( r \gt A_i \) 인 경우

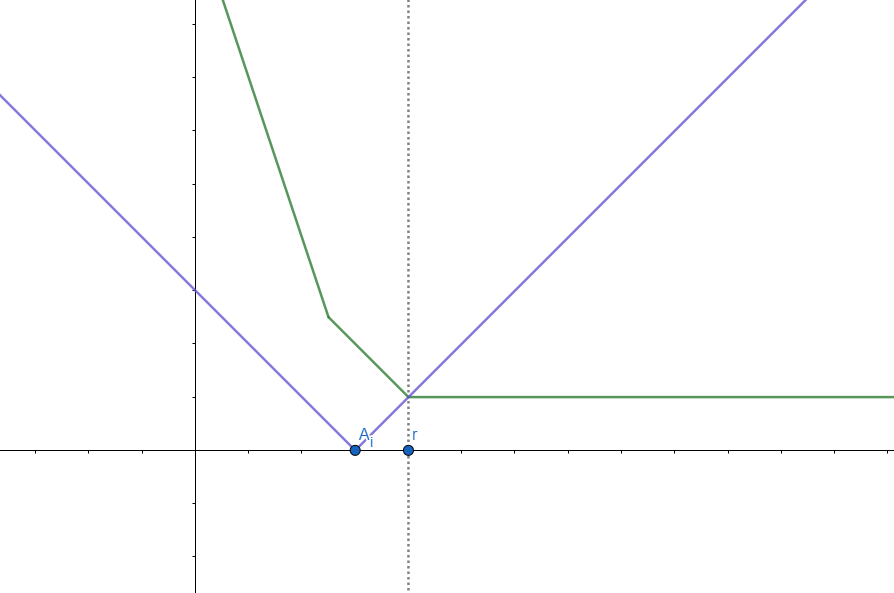
그림으로 나타내면 다음과 같다. 이 경우는 \(A_i\) 왼쪽 기울기가 \(1\) 감소하는 것은 동일하고, \(A_i\) 부터 \(r\) 사이 구간은 기울기가 \(1\) 증가하게 된다. 이 작업은 다음의 간단한 세 가지 과정을 통해 해결할 수 있다.

  1. \(A_i\)를 \(Q\)에 추가한다. 이러면 일단 \(A_i\) 왼쪽의 기울기가 \(1\) 감소한다.
  2. \(r\)을 \(Q\)에서 제거한다. 이러면, \(r\) 왼쪽의 기울기가 전부 \(1\) 증가하는 것과 같으므로 일단 \(A_i\) 에서 \(r\) 사이의 기울기가 \(1\) 증가하는 것은 해결했다. 하지만, \(A_i\) 보다 작은 지점까지도 전부 \(1\) 씩 증가하게 되므로 이걸 다시 감소시켜야 정확해진다.
  3. 따라서, \(A_i\)를 하나 더 \(Q\)에 추가한다. 이러면 \(A_i\) 이전의 기울기는 유지된다.

이 과정은 prefix sum을 응용해서 특정 구간에만 값을 \(1\) 증가시켜주는 것과 원리가 동일하므로 해당 과정을 생각하면 이해하기가 편하다. 따라서 이 동작은 세 번의 우선순위 큐 push, pop을 통해 해결가능하고 시간복잡도는 \(O(logN)\) 임도 알 수 있다.

또 한 가지 처리해야하는 것은, \(A_i\) 에서 \(r\) 위치까지 전부 함숫값이 \(1\)씩 증가하므로, 전체 함수의 최솟값 \(ans\)도 \(r - A_i\) 만큼 증가하게 된다는 것이다. 따라서 \(ans\) 값을 그만큼 증가시켜주면 된다.

위와 같은 과정을 \(A_2, \dots, A_n\)에 대해 반복시켜주고 나면 \(ans\) 에는 우리가 원하는 답이 들어가 있게 된다. 따라서 각 단계마다 \(O(logN)\) 시간이 걸리고 단계는 최대 \(O(N)\)번 반복되므로 \(O(NlogN)\)시간에 답을 구할 수 있다.

Codeforces #371 (Div.1) C. Sonya and Problem Without a Legend

위 문제가 바로 여기서 설명한 것과 완전히 동일한 방법을 이용해서 풀 수 있는 문제이다. 이 문제의 경우 \(N \le 3000\) 이고 다른 방법으로도 풀 수 있지만 여기서 설명한 방법을 연습하기에도 적절한 문제인 것 같다.

이 최적화 기법의 장점은 구현이 아주 간결하고 짧다는 것이다. 앞서 설명한 풀이를 그대로 구현한 위 문제의 정답 코드는 다음과 같다.

#include <stdio.h>
#include <vector>
#include <queue>
#include <algorithm>
#include <iostream>
#include <string>
#include <bitset>
#include <map>
#include <set>
#include <tuple>
#include <string.h>
#include <math.h>
#include <random>
#include <functional>
#include <assert.h>
#include <math.h>

using namespace std;

using i64 = long long int;

int main()
{
	int n;
	scanf("%d", &n);

	vector<i64> arr(n);

	for (int i = 0; i < n; i++)
		scanf("%lld", &arr[i]);

	priority_queue<i64> heap;
	i64 ans = 0;
	i64 loff = 0;

	heap.push(arr[0]);

	for (int i = 1; i < n; i++)
	{
		loff++;

		i64 lend = heap.top() + loff;

		if (arr[i] <= lend)
		{
			ans += lend - arr[i];
			heap.pop();
			heap.push(arr[i] - loff);
		}
		
		heap.push(arr[i] - loff);
	}

	printf("%lld\n", ans);

	return 0;
}

연습문제: NOI18_Safety

문제 링크

이 기법을 적용할 수 있는 또 다른 문제다(사실 나는 이걸로 먼저 배웠다). 위의 문제는 오름차순으로 만드는게 목표인데, 이 문제는 인접한 두 수 간의 차이를 \(k\) 이내로 만드는 것이 목표다.

방법이나 원리는 비슷하다. 다만 이 문제의 경우 기울기가 음수인 그래프의 좌측 부분만 관리하는 것으로는 풀 수 없고 기울기가 양수인 우측 부분도 같이 관리해주어야 한다. 하지만 기본적으로 대칭이라 관리하는 방법은 크게 다르지 않고, \(k\) 이내로 만든다는 조건 때문에 그래프의 좌측은 \(-k\)만큼 평행이동, 우측은 \(k\)만큼 평행이동시켜준다는 등의 사소한 차이점들이 있다.

이 문제를 직접 그래프를 그려서 위 풀이를 적용하고 해결하는 과정을 통해 이 기법을 좀 더 정확하게 이해하고 익힐 수 있을 것이다. 따라서 이 문제 풀이에 대한 자세한 설명은 생략한다. 앞의 문제와 비슷하게 이 문제도 풀이만 유도하고 나면 코드는 굉장히 간결하고 짧다.