[16663] Distance Sum
마지막 수정 시각: 2020-10-26 22:03:12
문제 요약
연결된 가중치 없는 무향 그래프가 주어진다. \( d(u,v) \) 를 정점 \(u\)와 \(v\) 사이의 최단 거리라고 할 때, 모든 \((u, v)\) 쌍에 대해 \(d(u,v)\)의 합을 구하여라. 정점 개수 \(n\)은 \(2\)이상 \(10^5\) 이하, 간선 개수 \(m\)은 \(n-1\)이상 \(n+42\) 이하.
풀이
\( m = n - 1 \)인 경우
트리일 때의 풀이를 먼저 생각해 보자. 트리인 경우 모든 정점 쌍에 대해 거리 합을 구하는 것은 널리 알려진 풀이가 있다. 트리에서 임의의 정점을 루트로 잡고, 각 트리에 대해 다음과 같은 함수를 생각해보자.
- \(C(root)\) : \(root\) 의 서브트리에 존재하는 정점의 개수 합
- \(D(root)\) : \(root\) 의 서브트리에 속하는 각 정점으로부터 \(root\)까지의 거리 합
이렇게 정의할 경우, 각 정점 \(v\)에 대해 \(C(v)\) 값과 \(D(v)\) 값은 트리를 한 번 dfs하면서 계산할 수 있다. \(C(v)\)의 경우 \(v\)의 모든 자식 \(ch\)에 대해 \(\sum C(ch) + 1\)이 되고, \(D(v)\) 의 경우 \(\sum D(ch) + C(ch)\) 가 된다. 이를 재귀적으로 반복하여 모든 \(C(v)\) 값과 \(D(v)\) 값을 계산했다고 하자.
이 때 식을 잘 정리해 보면 각각의 정점 \(v\)에 대해 그 정점의 임의의 한 자식 정점 \(x\)의 서브트리로부터 \(v\)를 거쳐, \(x\)의 서브트리에 속하지 않는 다른 정점 \(y\)로 가는 거리를 \(O(1)\)에 구할 수 있다. 이를 이용해 모든 정점 \(v\)에 대해 그 정점 \(v\)를 거쳐가는 정점 쌍들의 최단 거리 합을 그 정점의 자식 정점 개수에 비례하는 시간에 구할 수 있으므로, 총 시간복잡도 \(O(n + m)\)에 문제를 해결할 수 있다.
\( m = n \)인 경우
이 경우는 싸이클이 딱 하나 있는 그래프로 생각할 수 있다. 이 때, 이 그래프를 한 가운데 큰 싸이클이 있고, 그 싸이클에 트리가 주렁주렁 달려 있는 상태로 생각해보자.
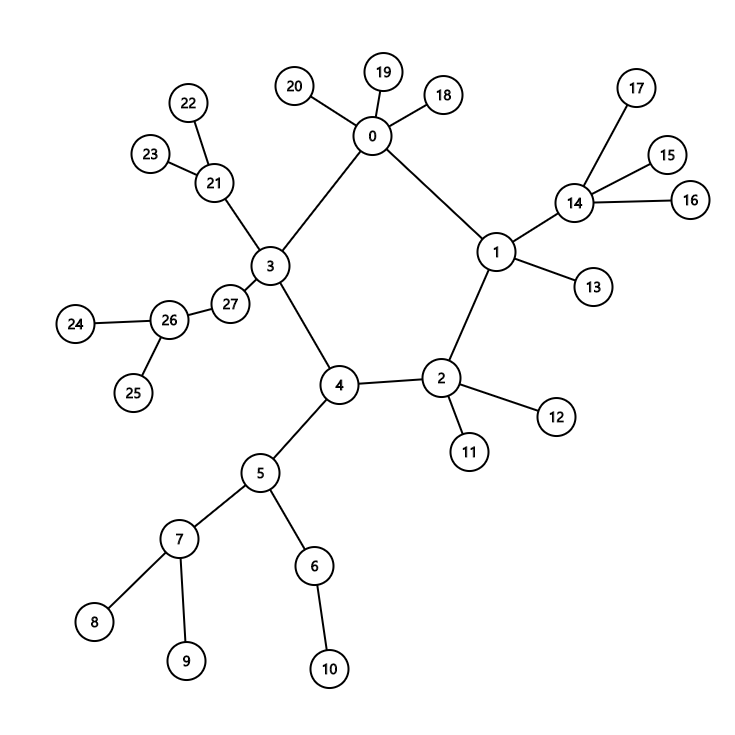
예를 들면 이런 형태. 가운데 0-1-2-4-3은 싸이클이고, 그 싸이클에 속하는 각 정점에 트리들이 주렁주렁 달려 있는 모양이다.
여기서, 싸이클 부분을 제외하고 트리 부분을 생각해보자. 싸이클에 속하는 각 정점이 트리의 루트 노드가 되고, 이 루트에 딸려있는 각각의 트리에 대해서는 \(m=n-1\) 일 때의 풀이를 이용해서 거리합을 구할 수 있다.
따라서, 싸이클을 제외한 부분에서는 답을 구할 수 있으므로 싸이클에 속하는 정점에 대해 빠르게 답을 구할 수 있다면 \(m=n\)일 때도 문제를 해결할 수 있다.
트리 부분은 고려 대상이 아니니 아예 제거하고, 트리의 각 루트(그래프에 속한 정점) \(v\)에 대해 \(D(v)\), \(C(v)\) 값을 계산해뒀다고 하자. 싸이클에서 두 정점간의 최단 거리를 구하는 것은 상대적으로 간단하다. 싸이클의 한 정점 \(x\)에서 다른 정점 \(y\)로 가는 경우의 최단 거리는 시계 방향으로 가는 것과 반시계 방향으로 가는 것중에 어느 쪽이 짧은 지를 골라서 선택하면 된다. 이 때, 싸이클에 속한 정점의 개수가 \(k\)개라고 하면 이 거리는 \(k/2\)를 넘을 수 없으므로, 임의의 정점 \(x\)에 대해 \(x\)에서 \(x\)다음 \(k/2\)개 정점으로 가는 최단거리를 순서대로 구해서 더해주면 답을 구할 수 있다.
이 때 싸이클의 한 정점 \(x\)에서 \(y\)로 가는 거리를 구하는게 실제로는 \(x\)의 서브트리에 속하는 임의의 정점에서 \(y\)의 서브트리에 속하는 임의의 정점으로 가는 거리 쌍의 합을 구하는 것이므로, \(D(v)\)와 \(C(v)\) 값을 이용해 적절한 식을 유도해서 답을 계산해야 한다.
이 경우도 마찬가지로 식을 잘 계산하면 싸이클의 모든 정점에 대해 거리 합을 싸이클의 크기 \(k\)에 비례하는 \(O(k)\) 시간에 구할 수 있으므로, 전체 시간 복잡도 \(O(n + m)\) 시간에 문제를 해결할 수 있다.
\( m > n \)인 경우
\(m = n\)까지 비교적 어렵지 않은 반면 여기서부터는 문제의 난이도가 확 증가한다. 마찬가지로, 트리인 부분은 미리 계산해서 제외해놓고 생각해보자. 트리 부분을 제외하고 보면 모든 정점의 차수(degree)가 2이상이 된다.
여기서 각 정점을 차수가 3이상인 경우와 2인 경우로 나눠서 생각하면, 차수가 3이상인 정점은 그렇게 많이 존재할 수 없다는 사실을 알 수 있다. 모든 정점의 차수가 2인 경우 전체가 하나의 싸이클을 이뤄 \(m = n\)인 상태가 되는데, 여기서 어떤 정점의 차수가 3이상이 되는 경우 서로 다른 싸이클이 여기에 덧붙는 형태가 되어 이런 정점이 하나 추가될 때마다 간선과 정점의 개수 차이가 최소한 하나씩은 벌어지게 된다. 문제 입력 제한에서 \(m \le n + 42 \)이므로 차수가 3이상인 정점이 많아야 40~50개 정도 밖에 되지 않을 것이라는 사실을 알 수 있다. 이 사실을 한 번 이용해보자. 차수가 2인 정점은 간단하게 생각해 일렬로 정점들이 늘어서서 연결되어 있는 형태인데, 이건 단순하게 생각하면 하나의 간선처럼 볼 수 있다.
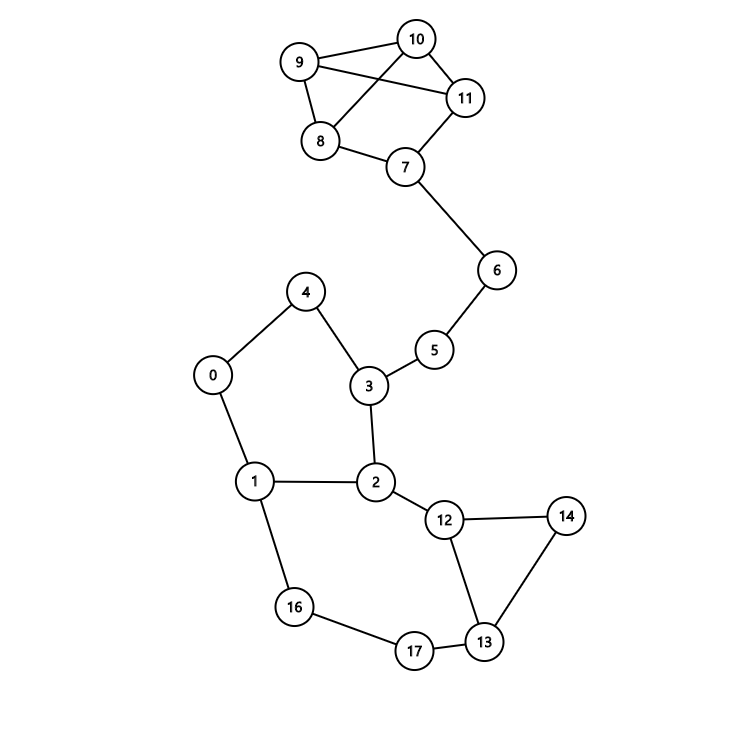
예를 들어 이런 그래프가 있다고 치고, 이 그래프를 차수가 3이상인 정점들만 정점으로 남겨두고, 차수가 2인 정점들의 연쇄로 이어져 있는 경우는 하나의 간선처럼 취급한다고 생각해 보자.
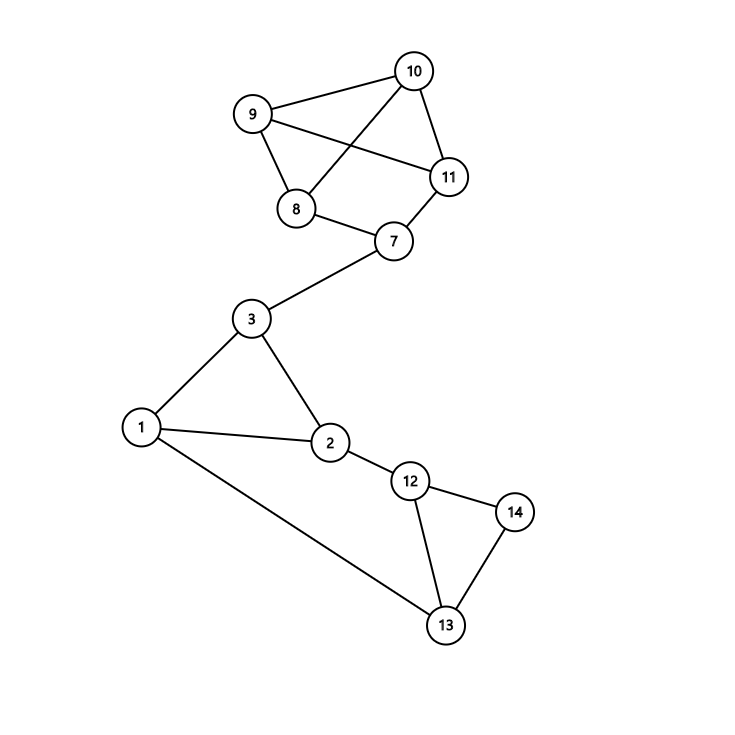
위 그림과 아래 그림을 잘 비교해보면 어디가 간선으로 바뀌었는지 알 수 있다. 이렇게 바꾸고 나면 이 그래프에서 모든 정점은 차수가 3이상이 되며 정점의 개수는 많아야 50개 정도인 그래프로 바뀌게 된다. 또, 이렇게 바꿨을 때 각 간선의 길이가 일정하지 않으므로 weighted graph가 된다.
이렇게 만든 그래프에서 모든 정점 쌍간의 거리는 플로이드 쌍 알고리즘 등을 이용해 \(O(N^3)\)에 구할 수 있다. 이 때 \(N=50\) 정도이므로(차수가 3인 정점의 개수) 아주 빠르게 동작하게 된다. 물론 마찬가지로 정점이 단순한 정점이 아니라 그 정점에 딸린 트리를 고려해야 하므로 공식은 잘 유도해서 사용해야 한다.
이제 차수가 3인 정점 쌍 간의 거리는 구했으므로 차수가 2인 정점과 3인 정점 쌍간의 거리 합, 차수가 2인 정점 쌍간의 거리 합을 구하면 문제를 해결할 수 있다. 이때 차수가 2인 정점과 3인 정점 쌍간의 거리는 임의의 차수가 3인 정점에서 시작해서 BFS 등의 방법을 이용해 다른 모든 차수가 2인 정점에 방문하면 답을 구할 수 있다. 이 경우 각각의 차수가 3인 정점에 대해 \(O(n)\)의 시간이 걸리지만, 차수가 3인 정점의 개수가 많지 않으므로 충분히 빠르게 동작하게 된다. 대충 \(O(50n)\) 정도.
마지막으로 차수가 2인 정점 쌍간의 거리만 구하면 문제를 해결할 수 있지만, 이 경우가 가장 어렵다. 여기서도 \(m = n\) 일 때 싸이클에서 어디까지가 최단 거리인지를 보고 한 번에 계산했던 것과 유사한 접근을 쓴다. 차수가 3인 두 정점 \(a\)와 \(b\)를 잇는 차수가 2인 정점열을 \(x_1, x_2, \dots, x_k\) 라고 하자. 즉, \(a, x_1, x_2, \dots, x_k, b\) 순으로 정점들이 연결되어 있는 일자 간선이다.
이 때 부분합 개념을 이용해서 전처리를 해둔다. \(A(i)\) 를 정점 \(a\)에서 \(x_1, x_2, \dots, x_i\) 까지의 최단거리 합이라고 하자. \(B(i)\) 는 반대로 \(x_i, x_{i+1}, \dots, x_k\)에서 정점 \(b\)까지의 최단거리 합. 이건 모든 일자 간선들에 대해 미리 전처리해 두는데 \(O(n)\)의 시간이면 충분하다.
다시 원래의 문제로 돌아와보자. 차수가 2인 임의의 두 정점이 같은 간선(정점들이 일자로 연결된)에 속하는 경우가 있고 서로 다른 간선에 속하는 경우가 있다. 같은 간선에 속하는 경우부터 생각해보자. 바로 위 문단에서 쓴 표기법을 이용하면, 정점열에서 임의의 \(x_i\)와 \(x_j\)간의 최단거리 합을 구하는 경우이다. 이 때, 같은 간선 내라고 해서 \(x_i, x_{i+1}, \dots, x_{j-1}, x_{j}\)의 경로로 이동하는 것이 항상 최단거리는 아니라는 점에 주의해야 한다. 역방향으로 돌아서 \(x_i \to a \to b \to x_j \)로 가는게 최단거리인 경우가 있다.
이걸 \(m=n\) 일 때 싸이클에서 시계방향으로 가는게 빠른지 반시계방향으로 가는게 빠른지 판단하는 것과 비슷하게 생각할 수 있다. 맨 처음에 차수가 3인 각각의 정점들에 대해 해당 정점 쌍간의 거리가 얼마인지 계산해두었으므로, \(x_i\)에서 시작해서 어디까지 가는게 돌아서 가는것보다 빠른지 \(O(1)\)에 계산할 수 있다. 또, 부분합 개념을 이용해 연속한 정점들간의 거리 합을 전처리해두었으므로, 이를 이용해 특정 \(a_i\)에서 \(a_{i+1}, a_{i+2}, \dots, a_j\) 까지의 거리 합도 \(O(1)\)에 구할 수 있다. 따라서 같은 간선 내에 속하는 정점간의 최단 거리 합은 마찬가지로 \(O(n)\)에 구할 수 있다.
이제 서로 다른 간선에 속한 두 정점 \(x, y\)에 대해 최단거리를 계산하는 경우를 생각해보자. 이 경우 임의의 정점들을 잡아서는 시간 안에 답을 구할 수 없기 때문에, 하나의 정점 \(x\)와 다른 임의의 간선 \(a \to b\)를 골라서 해당 정점 \(x\)로부터 간선 \(a \to b\)에 속하는 모든 정점 \(y\)에 대한 답을 한 번에 구하는 방식으로 계산할 것이다. 이렇게 계산할 경우 (정점 개수) * (일자 간선 개수) 만큼의 시간이 걸린다. 그렇지만 이 경우도 차수가 3인 정점의 개수 상한이 작기 때문에 마찬가지로 충분히 빠르게 동작한다. 간선 개수는 최대 정점 개수의 제곱이므로, 많아야 \(2000n\) 정도 반복이 필요하다고 생각할 수 있다.
정점 \(x\)와 간선 \(a \to b\)를 뽑았을 경우도 마찬가지로 비슷하게 계산할 수 있다. \(a \to b\)에 속하는 임의의 정점 \(y\)에 대해, \(x \to a \to y\)로 가는게 빠른 경우와 \(x \to b \to y\)로 가는게 빠른 경우 두 가지가 있다. 이 두 가지의 경계가 되는 인덱스를 찾으면 마찬가지로 전처리해 둔 부분합 배열을 이용해 \(O(1)\) 시간에 답을 구할 수 있고, 이러한 경계를 찾는 것 역시 앞서 계산해둔 차수가 3인 정점들간의 거리 배열을 이용하면 \(O(1)\) 시간에 구할 수 있다.
따라서, 전체 시간복잡도 \(O(n + m)\) (물론 상수가 매우 큰) 에 문제를 해결할 수 있다. 아이디어가 어렵다기보다는 구현이 굉장히 어렵고 식을 정확하게 잘 유도해야 하는 문제였다.
